本文共 9486 字，大约阅读时间需要 31 分钟。

T1：花园

title

小 L 有一座环形花园，沿花园的顺时针方向，他把各个花圃编号为 1∼n。花圃 1 和 n 是相邻的。

他的环形花园每天都会换一个新花样，但他的花园都不外乎一个规则：任意相邻 m 个花圃中都只有不超过 k 个 C 形的花圃，其余花圃均为 P 形的花圃。 例如，若 n=10 , m=5 , k=3 ，则 CCPCPPPPCC 是一种不符合规则的花圃。 CCPPPPCPCP 是一种符合规则的花圃。 请帮小 L 求出符合规则的花园种数对 109+7 取模的结果。 【输入格式】 只有一行三个整数，分别表示 n, m, k。 【输出格式】 输出一行一个整数表示答案。 【样例1】 garden.in garden.out 10 5 3 458 【样例2】 garden.in garden.out 6 2 1 18 【数据规模与约定】 对于 40% 的数据，保证 n≤20。 对于 80% 的数据，保证 n≤105。 对于 100% 的数据，保证 2≤n≤1015 ，2≤m≤min(n,5)，1≤k≤m。

solution

不得不说一句，这个出题人是很有良心的

---

首先40分，直接暴力枚举出每一种花圃装修，然后进行$check$

---

接着80分，看数据范围就可以明显被$n,m$的量级差给冲击到，$m$极其小，花圃不是$C$就是$P$

顺其自然的联想到状压$dp$求解，设$dp[i][s]$表示到第$i$个花圃为止，最后连续的$m$个花圃状态为$s$ $$dp[i][s]=\sum _{s=0}^{(1<<m)-1}dp[i-1][s]$$ 当然这中间的转移需要判断一下$s$中是否$1$过多（假设$C$为1） 两者是否有转移关联性，因为对于$i$而言的前$m-1$个花圃应该是与$i-1$的后$m-1$个花圃是一样的

---

最后100分

显而易见，我们需要消除掉$n$带来的巨大不可承受的时间复杂度，一般来说这么大的$n$ 要么发现实现根本与$n$不挂钩（通过某些转移方程式），要么压缩成$log$，亦或各种优化 在80分状压的时候，我画了个示意图，要求转移之间某些花圃必须一一对应，连线段之间的相同 让我的灵感一瞬闪过——矩阵快速幂！！！

只要两个之间可以转移我就置为$1$，最后把对角线的值加起来即可

code

#include 
   
    #include 
    
     using namespace std;#define mod 1000000007#define ll long longll n, ans;int m, k, cnt;int t[205];bool count( int S ) {   	int tot = 0;	while( S ) tot += S & 1, S >>= 1;	return tot > k;}bool comp( int s1, int s2 ) {   	for( int i = 0;i <= m - 2;i ++ ) {   		int x1 = ( s1 >> i ) & 1;		int x2 = ( s2 >> ( i + 1 ) ) & 1;		if( x1 != x2 ) return 1;	}	return 0;}struct Matrix {   	ll c[50][50];		Matrix() {   		memset( c, 0, sizeof( c ) );	}		Matrix operator * ( const Matrix &p ) {   		Matrix res;		for( int i = 1;i <= cnt;i ++ )			for( int k = 1;k <= cnt;k ++ )				for( int j = 1;j <= cnt;j ++ )					res.c[i][j] = ( res.c[i][j] + c[i][k] * p.c[k][j] % mod ) % mod;		return res;	}	}A, B;Matrix qkpow( Matrix x, ll y ) {   	Matrix res;	for( int i = 1;i <= cnt;i ++ ) res.c[i][i] = 1;	while( y ) {   		if( y & 1 ) res = res * x;		x = x * x;		y >>= 1;	}	return res;}int main() {   	scanf( "%lld %d %d", &n, &m, &k );	int S = 1 << m;	for( int i = 0;i < S;i ++ )		if( count( i ) ) continue;		else t[++ cnt] = i;	for( int i = 1;i <= cnt;i ++ )		for( int j = 1;j <= cnt;j ++ )			if( comp( t[i], t[j] ) ) continue;			else A.c[i][j] = 1;	B = qkpow( A, n );	for( int i = 1;i <= cnt;i ++ )		ans = ( ans + B.c[i][i] ) % mod;	printf( "%lld", ans );	return 0;}
    
   

T2：月亮神树

title

JM今天过得实在是太惨了，他肥肠不爽，因此他搬出了他祖传的月亮神树。月亮神树的光辉照耀XJTUACM，每分钟都可以从所有被照射的人的手中夺取他1%的财产。JM觉得他很快就能赚得盆满钵满。然而月亮神树不久后突然失控了，不仅不把它夺来的财产交给JM，甚至开始夺取JM的财产，把JM气疯了，赶紧关闭了月亮神树。

因为月亮神树没运行多久就被关掉了，所以大家并没有损失多少，迫于月亮神树的威压，并没有人去理它。可是wzk昨天刚中了彩票，赚了100000000000￥，转眼就被剥夺了很多。因为wzk太rich了，所以他的损失格外大。为了夺回财产，无敌的wzk决定消灭月亮神树。 月亮神树的构造非常神奇，它的枝杈交错纵横，树上甚至存在环路，可以视为一个无向带权连通图的结构。月亮神树有一个核心节点，记为 s 。要想消灭月亮神树，必须找到月亮神树的严格最不科学生成树，这是它的弱点，这样就能将其一举摧毁。 定义：一个图 G 的不科学生成树是 G 的一棵子树，在这棵子树上，从核心节点 s 到任意一个节点 u 的最短路径长度，和在原图上是等长的。其中节点 s 是月亮神树的核心节点。 定义：一个图 G 的最不科学生成树是 G 的所有不科学生成树中，边权和最小的一棵树。 定义：一个图 G 的严格最不科学生成树是 G 的所有最不科学生成树中，有序边序列的字典序最小的一棵树。 定义：一个图 G 的有序边序列是指，将图上所有边按编号从小到大排序后得到的编号序列。当然，子图子树也适用。 现在给定月亮神树，即给定一个 n 个点 m 条边的无向带权连通图，点的编号从1到n，边的编号从1到m，给定核心节点的编号 s ，求其严格最不科学生成树。   【输入格式】 第一行三个正整数 n,m,s 。 接下来 m 行，第 i 行三个正整数 u,v,w ，表示编号为 i 的边。 输入保证图是连通的，保证图上不含重边和自环。。 【输出格式】 第一行两个正整数 cnt 和 sum ，用空格隔开，其中 cnt 表示严格最不科学生成树的边的个数， sum 表示严格最不科学生成树的边权和。 接下来一行 cnt 个正整数，用空格隔开，为树上所有边的编号，按编号从小到大输出。 【样例1】 moontree.in moontree.out 3 3 3 1 2 1 2 3 1 1 3 2 2 2 1 2 【样例2】 moontree.in moontree.out 4 4 4 2 3 1 1 2 1 3 4 1 4 1 2 3 4 1 3 4 【数据规模与约定】 对于25%的数据， 1≤n,m≤10 。 另有25%的数据， 1≤n,m≤100 。 对于100%的数据， 1≤n,m≤3*105 ，1≤wi≤109 。

solution

老师说这道题最水，可我这道题的分最少

听完题解后觉得——确实很水 堆优化$dijkstra$时间复杂度$O(nlogn)$凸(艹皿艹 )！！！考试时我就想着先求出最短路，但我想着$dijkstra$时间复杂度不是$O(n^2)$唛，我连堆优化写法都想好了！！但是我败在了时间复杂度上面，我就没敲，靠！！一直写的这种，我竟不知是堆优化，鸭血！！！

---

首先跑出每个点距离超级源点的最短路，然后思考对于每个点可能存在不止一条最短路

此时就要保证权值最小，权值最小的保证下又要编号最小 所以当同时多条最短路出现时，取权值最小，更新编号数组 权值一样时，选编号更小者即可

---

code

#include 
   
    #include 
    
     #include 
     
      #include 
      
       #include 
       
        using namespace std;#define ll long long#define MAXN 300005struct Gragh {   	int v, id;	ll w;	Gragh(){   }	Gragh( int V, ll W, int ID ) {   		v = V, w = W, id = ID;	}};struct node {   	int v;	ll w;	node(){   }	node( int V, ll W ) {   		v = V, w = W;	}	bool operator < ( const node &t ) const {   		return w > t.w;	}};struct edge {   	int u, v, id;	ll w;	edge(){   }	edge( int U, int V, ll W, int ID ) {   		u = U, v = V, w = W, id = ID;	}}E[MAXN];priority_queue < node > q;vector < Gragh > G[MAXN];int n, m, s, tot, cnt;ll ans;int flag[MAXN];ll dis[MAXN];bool vis[MAXN], used[MAXN];void dijkstra() {   	memset( dis, 0x3f, sizeof( dis ) );	dis[s] = 0;	q.push( node( s, 0 ) );	while( ! q.empty() ) {   		int u = q.top().v; q.pop();		if( vis[u] ) continue;		vis[u] = 1;		for( int i = 0;i < G[u].size();i ++ ) {   			int v = G[u][i].v, w = G[u][i].w, id = G[u][i].id;			if( dis[v] > dis[u] + w ) {   				dis[v] = dis[u] + w;				q.push( node( v, dis[v] ) );				flag[v] = id;			}			else if( dis[v] == dis[u] + w ) {   				if( w < E[flag[v]].w ) flag[v] = id;				else if( w == E[flag[v]].w && id < E[flag[v]].id )					flag[v] = id;			}		}	}}int main() {   	scanf( "%d %d %d", &n, &m, &s );	for( int i = 1;i <= m;i ++ ) {   		int u, v; ll w;		scanf( "%d %d %lld", &u, &v, &w );		G[u].push_back( Gragh( v, w, i ) );		G[v].push_back( Gragh( u, w, i ) );		E[i] = edge( u, v, w, i );	}	dijkstra();	for( int i = 1;i <= n;i ++ )		if( flag[i] ) {   			++ tot, ans += E[flag[i]].w;			used[flag[i]] = 1;		}	printf( "%d %lld\n", tot, ans );	for( int i = 1;i <= m;i ++ )		if( used[i] ) printf( "%d ", i );	return 0;}
       
      
     
    
   

T3：保护出题人

title

出题人铭铭认为给 SDOI2012 出题太可怕了，因为总要被骂，于是他又给 SDOI2013 出题了。

参加 SDOI2012 的小朋友们释放出大量的僵尸，企图攻击铭铭的家。而你作为 SDOI2013的参赛者，你需要保护出题人铭铭。 僵尸从唯一一条笔直道路接近，你们需要在铭铭的房门前放置植物攻击僵尸，避免僵尸碰到房子。第一关，一只血量为 a1 点的僵尸从距离房子 x1 米处匀速接近，你们放置了攻击力为 y1点/秒的植物进行防御；第二关，在上一关基础上，僵尸队列排头增加一只血量为 a2 点的僵尸，与后一只僵尸距离 d 米，从距离房子 x2 米处匀速接近，你们重新放置攻击力为y2 点/秒的植物；……；第 n 关，僵尸队列共有 n 只僵尸，相邻两只僵尸距离 d 米，排头僵尸血量为 an 点，排第二的僵尸血量 an-1 ，以此类推，排头僵尸从距离房子 xn 米处匀速接近，其余僵尸跟随排头同时接近，你们重新放置攻击力为 yn 点/秒的植物。 每只僵尸直线移动速度均为 1 米/秒，由于植物射击速度远大于僵尸移动速度，可忽略植物子弹在空中的时间。所有僵尸同时出现并接近，因此当一只僵尸死亡后，下一只僵尸立刻开始受到植物子弹的伤害。 游戏得分取决于你们放置的植物攻击力的总和，和越小分数越高，为了追求分数上界，你们每关都要放置攻击力尽量小的植物。 作为 SDOI2013 的参赛选手，你们能保护出题人么？ 【输入格式】 第一行两个空格隔开的正整数 n 和 d，分别表示关数和相邻僵尸间的距离。 接下来 n 行每行两个空格隔开的正整数，第 i + 1 行为 ai和 xi，分别表示相比上一关在僵尸队列排头增加血量为 ai 点的僵尸，排头僵尸从距离房子 xi 米处开始接近。 【输出格式】 一个数，n 关植物攻击力的最小总和 ，保留到整数。   【样例1】 protect.in protect.out 5 2 3 3 1 1 10 8 4 8 2 3 7

【样例1 说明】

第一关：距离房子 3 米处有一只血量 3 点的僵尸，植物最小攻击力为 1.00000； 第二关：距离房子 1 米处有一只血量 1 点的僵尸、3 米处有血量 3 点的僵尸，植物最小攻击力为 1.33333； 第三关：距离房子 8 米处有一只血量 10 点的僵尸、10 米处有血量 1 点的僵尸、12 米处有血量 3 点的僵尸，植物最小攻击力为 1.25000； 第四关：距离房子 8 米处有一只血量 4 点的僵尸、10 米处有血量 10 点的僵尸、12 米处有血量 1 点的僵尸、14 米处有血量 3 点的僵尸，植物最小攻击力为 1.40000； 第五关：距离房子 3 米处有一只血量 2 点的僵尸、5 米处有血量 4 点的僵尸、7 米处有血量 10 点的僵尸、9 米处有血量 1 点的僵尸、11 米处有血量 3 点的僵尸，植物最小攻击力为 2.28571。 【数据规模与约定】 对于 30%的数据，n≤103 。 对于 50%的数据，n≤104 。 对于 70%的数据，1≤n≤105 ，1≤d≤106 ，1≤x≤106 ，1≤a≤106 。 对于 100%的数据， 1≤n≤105 ，1≤d≤1012 ，1≤x≤1012 ，1≤a≤1012 。

solution

此题的$x,a$我们可以抽象在二维平面上，就很想我们做的三分灯泡模型↓↓

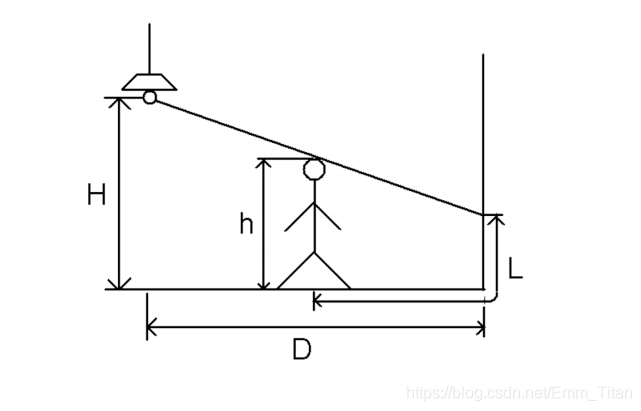设$dp[i][j]$表示消灭第$i$关卡前$i-j$个僵尸所需要的攻击力 为了保证自己不被吃掉，我们就要求第$i$关卡的$maxdp[i][j]$ 对于$j$而言，攻击力要求为$$(a_i+a_{i-1}+...+a_j)/(x_i+d\ast (i-j))$$ 对于另一个$k$而言，假设$j<k$，则攻击力要求为 $$(a_i+a_{i-1}+...a_j+...a_k)/(x_i+d\ast (i-j+j-k))$$ 令$A=a_i+a_{i-1}+...+a_j,B=x_i+d\ast (i-j)$ 则两个式子分别为 $$A/B,(A+a_{j-1}+...+a_k)/(B+d\ast (j-k))$$ 交叉相成 $$A\ast B+A\ast d\ast (j-k),A\ast B+B\ast (a_{j-1}+...+a_k)$$ 相抵消 $$A\ast d\ast (j-k),B\ast (a_{j-1}+...a_k)$$ 在转化 $$A/B,(a_{j-1}+...+a_k)/(d\ast (j-k))$$ 最后推出我们想要的方程式 y i ​ = ( 1 ≤ j ≤ i )    m a x ​ { ( s u m i ​ − s u m j − 1 ​ ) / ( x i ​ + d × ( i − j ) } y_i​=(1≤j≤i)\ \ max​\{(sum_i​−sum_{j−1}​)/(x_i​+d×(i−j)\} yi​​=(1≤j≤i)  max​{

(sumi​​−sumj−1​​)/(xi​​+d×(i−j)} 类似于斜率优化一样去维护一个下凸包，然后三分找最大斜率即可

code

#include 
   
    #include 
    
     using namespace std;#define MAXN 100005int n, top;double ans;long long d;int st[MAXN];long long x[MAXN], a[MAXN], sum[MAXN];double calc1( int i, int j ) {   	return 1.0 * ( sum[i - 1] - sum[j - 1] ) / ( d * ( i - j ) );}double calc2( int i, int j ) {   	return 1.0 * ( sum[i] - sum[j - 1] ) / ( x[i] + d * ( i - j ) );}int main() {   	scanf( "%d %lld", &n, &d );	for( int i = 1;i <= n;i ++ ) {   		scanf( "%lld %lld", &a[i], &x[i] );		sum[i] = sum[i - 1] + a[i];	}	for( int i = 1;i <= n;i ++ ) {   		while( top > 1 && calc1( i, st[top] ) < calc1( st[top], st[top - 1] ) )			top --;		st[++ top] = i;		int l = 1, r = top;		while( l <= r ) {   			int tmp = ( r - l + 1 ) / 3;			int mid1 = l + tmp - 1, mid2 = l + ( tmp << 1 ) - 1;			if( mid1 == mid2 ) break;			if( calc2( i, st[mid1] ) < calc2( i, st[mid2] ) ) l = mid1 + 1;			else r = mid2 - 1;		}		ans += max( calc2( i, st[l] ), calc2( i, st[r] ) );	}	printf( "%0.f", ans );	return 0;}
    
   

转载地址：http://rxil.baihongyu.com/